概述

本章首先介绍“知识与知识表示”的概念，然后介绍“谓词逻辑、产生式、框架、语义网络”等当前人工智能中应用广泛的知识表示方法。然后，简要介绍知识图谱，为后面介绍推理方法、专家系统等奠定基础。

知识 - 概念

  • 知识是在长期的生活及社会实践中、在科学研究及实验中积累起来的对客观世界的认识与经验。
  • 把有关信息关联在一起所形成的信息结构成为知识。
  • 知识反映了客观世界中事物之间的关系，不同事物或者相同事物间的不同关系形成了不同的知识

image-20240716233245951

“雪是白色的。” ——这一条知识被称为“事实”

如果 头痛且流涕，则 有可能患了感冒。

—用“如果…，则…”关联起来形成的知识称为“规则

知识 - 特性

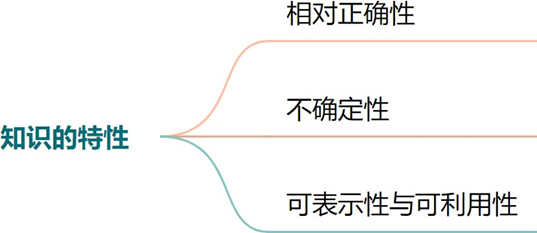
image-20240716233305923

相对正确性 不确定性 可表示性与可利用性
任何知识都是在一定的条件及环境下产生的，在这种条件及环境下才是正确的。 举例：“1+1=2” 十进制的条件下正确，二进制的条件下不正确 随机引起的不确定性—“如果头痛且流涕，则有可能患了感冒”模糊性引起的不确定性— 风的强弱、雨的大小经验引起的不确定性—经验性自身就蕴含着不精确性及模糊性，这就形成了知识的不确定性不完全性引起的不确定性—“火星上可能有生命？” 知识的可表示性: 知识可以用适当形式表示出来，如用“语言、文字、图形、神经网络”等。 知识的可利用性: 知识可以 被利用。

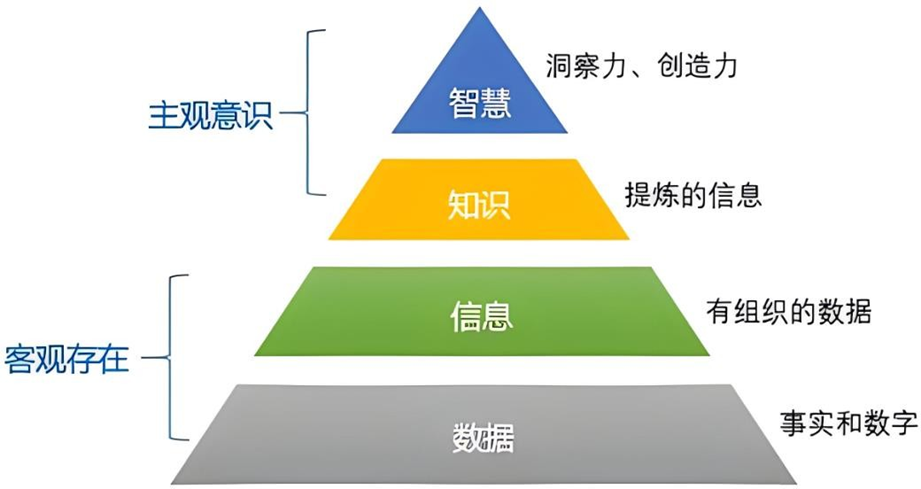
知识 - 与“数据、信息和智慧”的关系

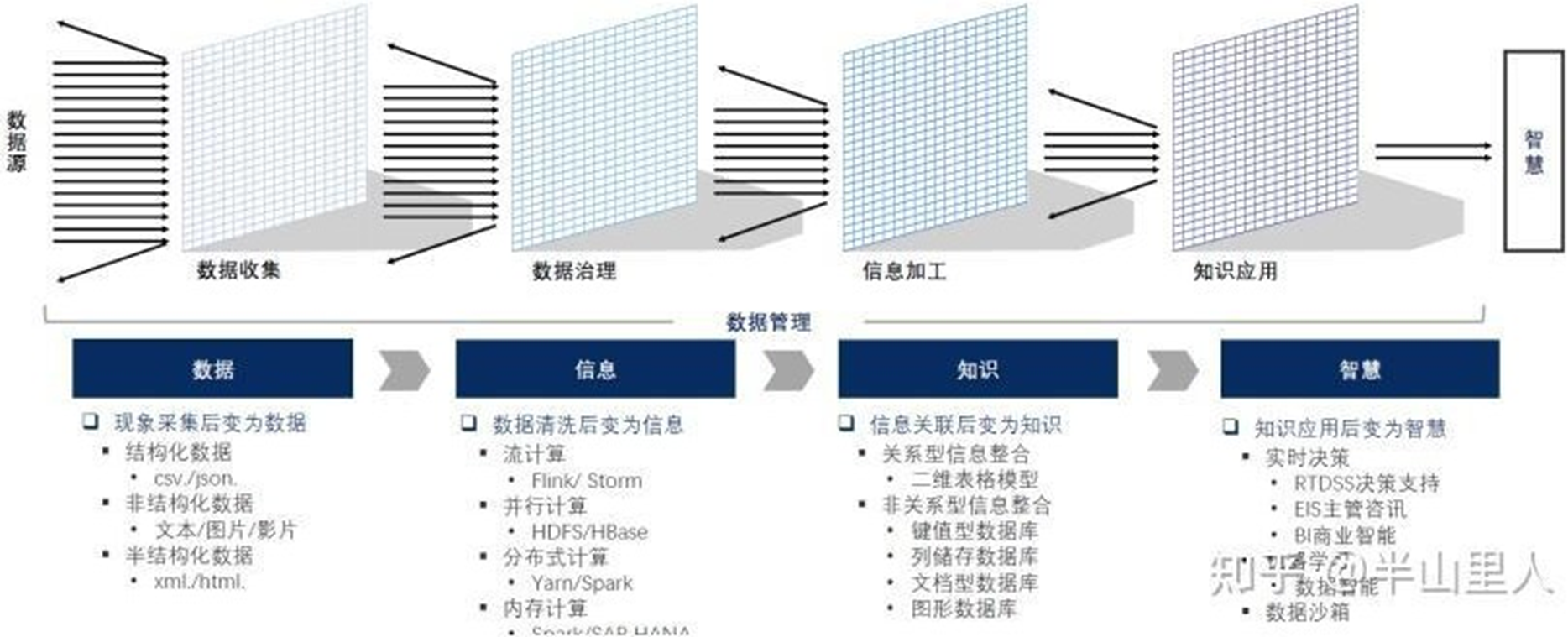
image-20240716233455683

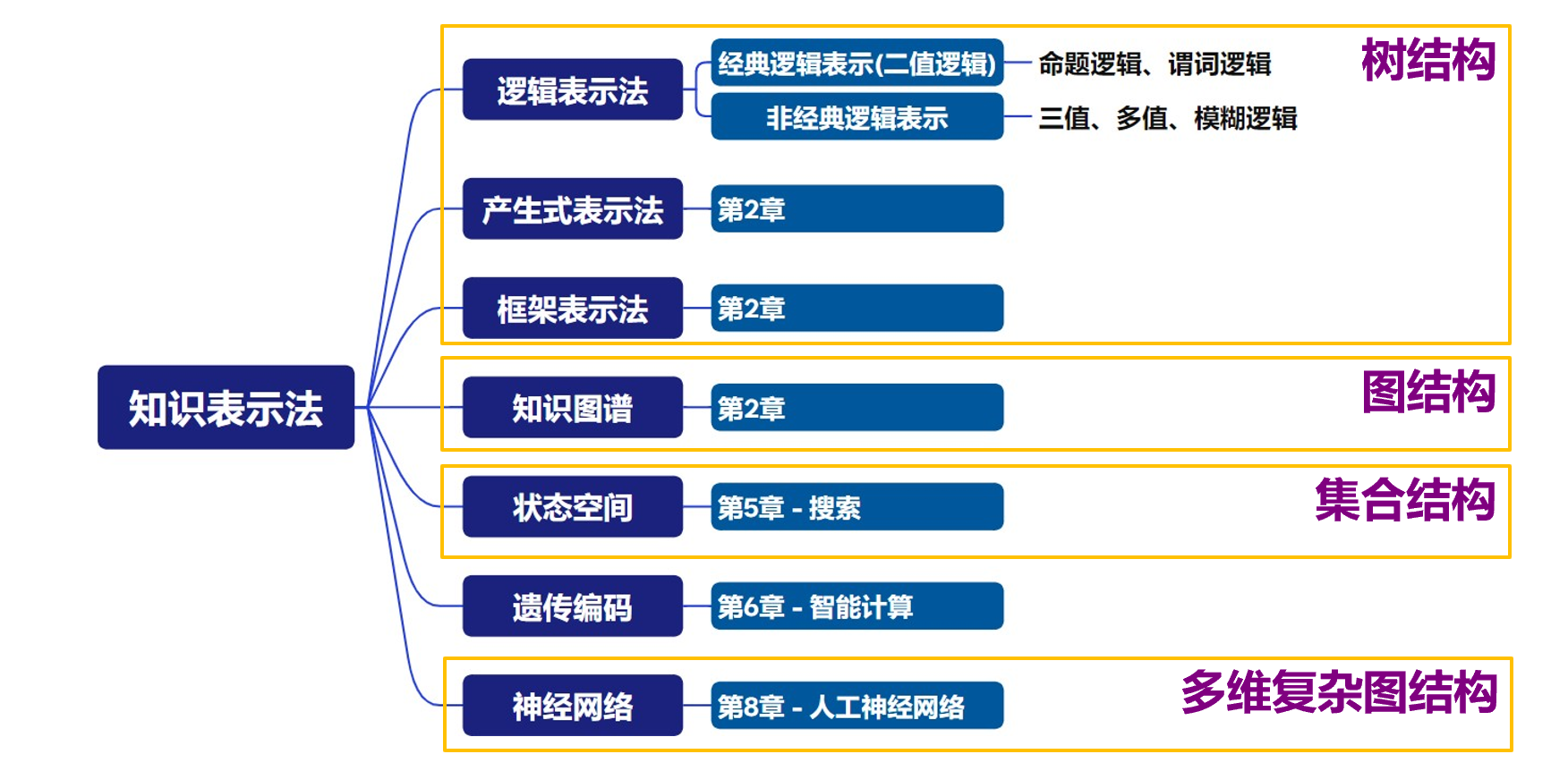
知识的表示 - 定义与分类

知识表示：将人类知识形式化或者模型化。是对知识的一种描述，或者说是一组约定，一种计算机可以接受的用于描述知识的数据结构。

image-20240716233545994

逻辑表示法 - 在AI中的重要性

  • 人类思维活动一个重要功能是逻辑推理，即通过演绎和归纳等手段对现有观测现象进行分析，得出判断。
  • 在人工智能发展初期，脱胎于逻辑推理的符号主义人工智能(symbolicAI)是人工智能研究的一种主流学派。
  • 符号主义认为：所有概念均可通过人类可理解的“符号”及符号间关系来表示。
  • 符号主义假设：可通过逻辑方法来对符号及其关系进行计算，实现逻辑推理，辨析符号所描述内容是否正确。
  • 命题逻辑与谓词逻辑是最先应用于人工智能的两种逻辑，在知识的形式化表示方面，特别是定理的自动证明方面，发挥了重要作用，在人工智能的发展史中占有重要地位。

逻辑表示法 – 定义、作用与分类

  • 定义：逻辑是用数学方法来研究关于推理和证明等问题的研究。
  • 作用：逻辑是探索、阐述和确立有效推理原则的学科。

image-20240716233629999

提出了演绎推理中“三段论”方法的古希腊学者亚里士多德被誉为 “逻辑学之父”。

image-20240716233634328

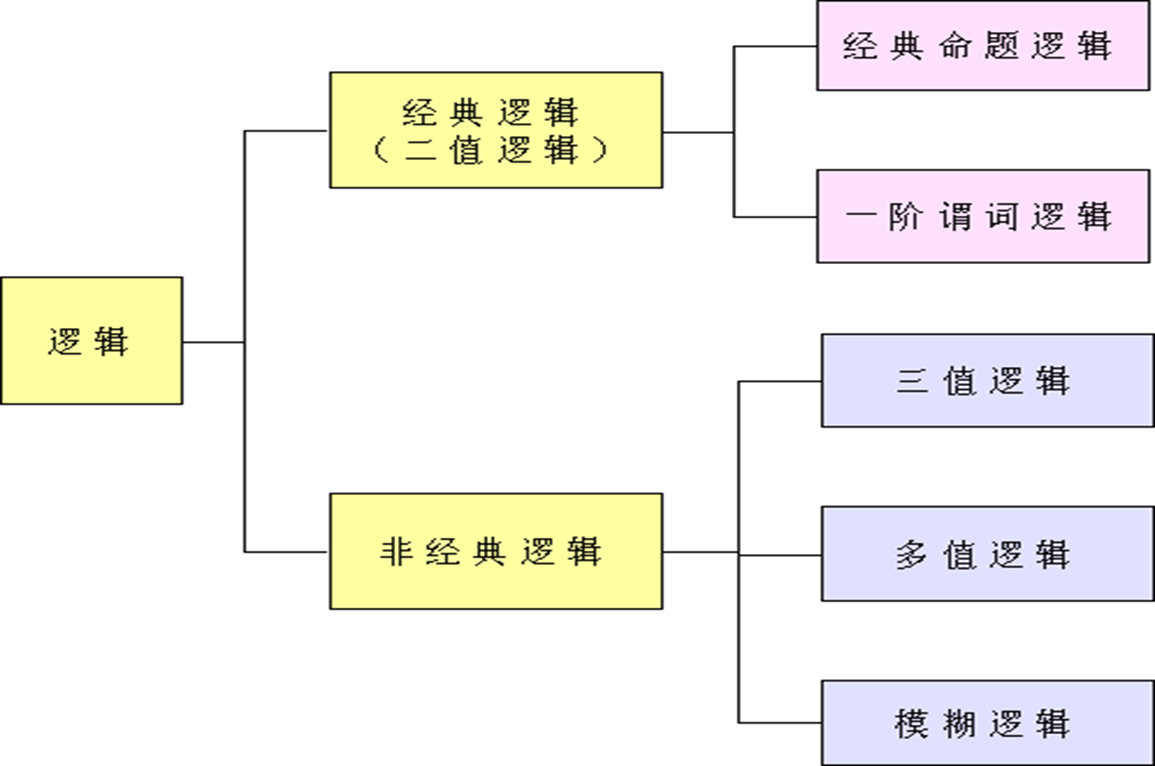
命题逻辑 – 概念

  • 命题（proposition）：一个非真即假的陈述句。
  • 命题逻辑：研究命题及命题之间关系的符号逻辑系统。是应用一套形式化规则对以符号表示的描述性陈述进行推理的系统。
  • 原子命题：一个或真或假的描述性陈述。
  • 复合命题：若干原子命题通过逻辑运算符而构成。
  • 命题联结词(connectives）
命题连接符号 表示形式 意义
与(and) 𝑝⋀𝑞 命题合取(conjunction)，即 “𝑝且𝑞”
或(or) 𝑝⋁𝑞 命题析取(disjunction)，即 “𝑝或𝑞”
非（not） ¬𝑝 命题否定(negation)，即 “非𝑝”
条件(conditional) 𝑝 → 𝑞 命题蕴含(implication)，即 “如果𝑝 则𝑞”
双向条件(bi-conditional) 𝑝 𝑞 命题双向蕴含(bi- implication)，即“𝑝当且仅当𝑞”

命题逻辑 - 复合命题的逻辑形式及逻辑值

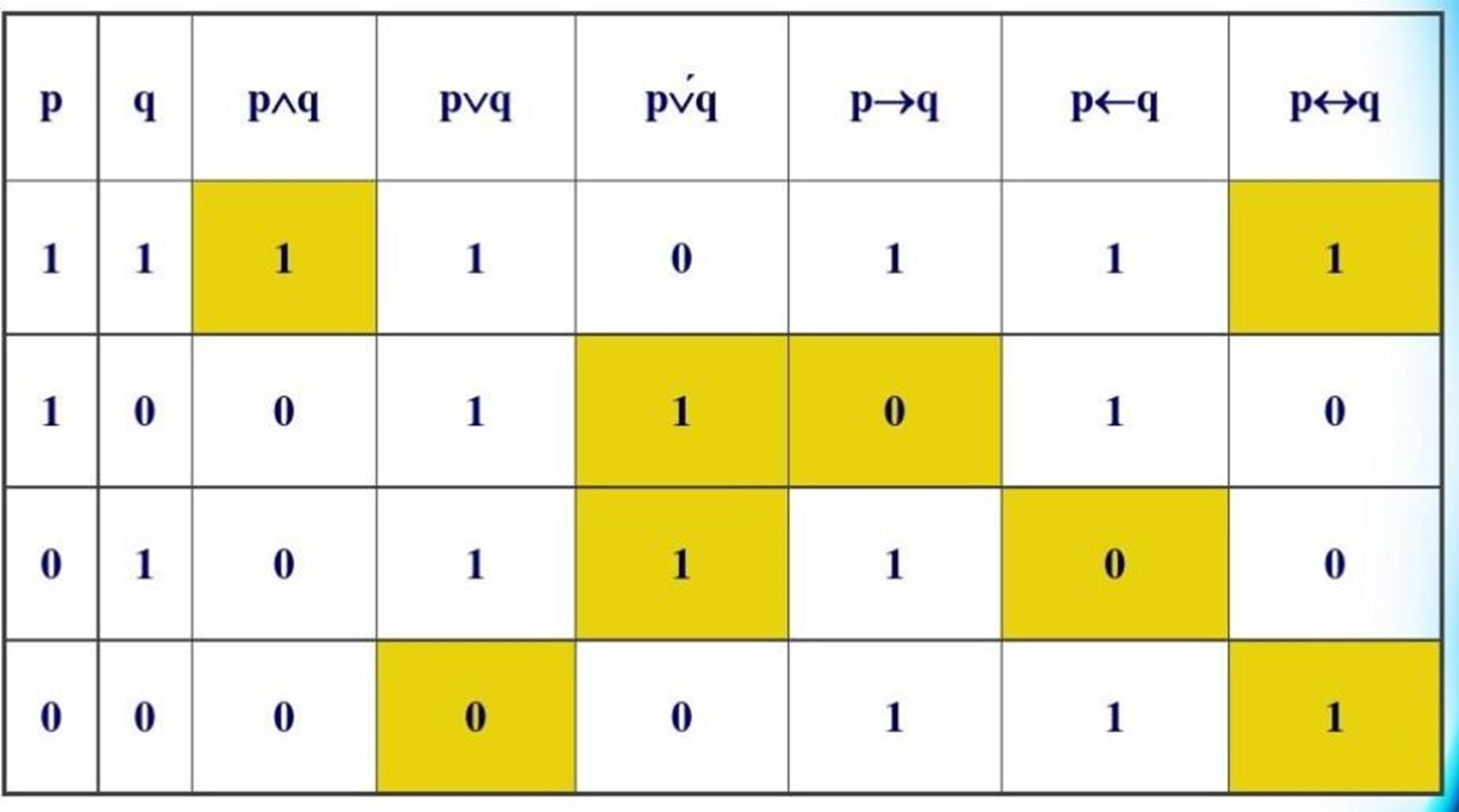
image-20240716233732286

命题逻辑 – 推理规则

image-20240717000338689

谓词逻辑 – 从命题逻辑到谓词逻辑

命题逻辑的局限性（缺点）

  • 描述能力有限：无法把它所描述的事物的结构及逻辑特征反映出来，也不能把不同事物间的共同特征表述出来。
  • 原子命题不可分解：每个陈述句是最基本的单位(即原子命题)，无法对原子命题进行分解。

造成问题

在命题逻辑中，不能表达“局部与整体、一般与个别”的关系。所以需要引入更加强大的逻辑表示方法，这就是“谓词逻辑”！

谓词逻辑 – 概念

  • 谓词

    • 谓词名：用于刻画个体的性质、状态或个体间的关系。
    • 个体：某个独立存在的事物或某个抽象的概念。

  • 谓词逻辑：研究内容是将原子命题进一步细化，分解出“个体、谓词和量词”，来表达“个体与总体的内在联系和数量关系”。它有以下三个核心概念：

    • 个体：可以是常量，也可以是变元，还可以是一个函数。
    • 谓词
    • 量词

谓词的一般形式

image-20240716233907195

函数与谓词的区别

函数是从定义域到值域的映射

谓词是从定义域到{𝑇𝑟𝑢𝑒,𝐹𝑎𝑙𝑠𝑒}的映射

谓词逻辑 – 连接词

无论是命题逻辑还是谓词逻辑，均可用下列连接词把一些简单命题连接起来构成一个复合命题，以表示一个比较复杂的含义。

﹁： “否定”（ negation）或 “非”。 “机器人不在2号房间”：﹁Inroom(robot,r2)
∨： “析取”（disjunction）——或。 “李明打篮球或踢足球”：Plays(Liming,basketball)∨Plays(Liming,football)
∧： “合取”（conjunction）——与。 “我喜欢音乐和绘画”：Like(I,music)∧Like(I,painting)
→：“蕴含”(implication)或 “条件”(condition)。 P→Q：“P蕴涵Q”“如果P，则Q” “如果刘华跑得最快，那么他取得冠军。” ：RUNS(Liuhua，faster)→WINS(Liuhua，champion)
：“等价”（equivalence）或“双条件”（bicondition）。PQ: “P当且仅当Q”。 “P仅当Q”：P Q

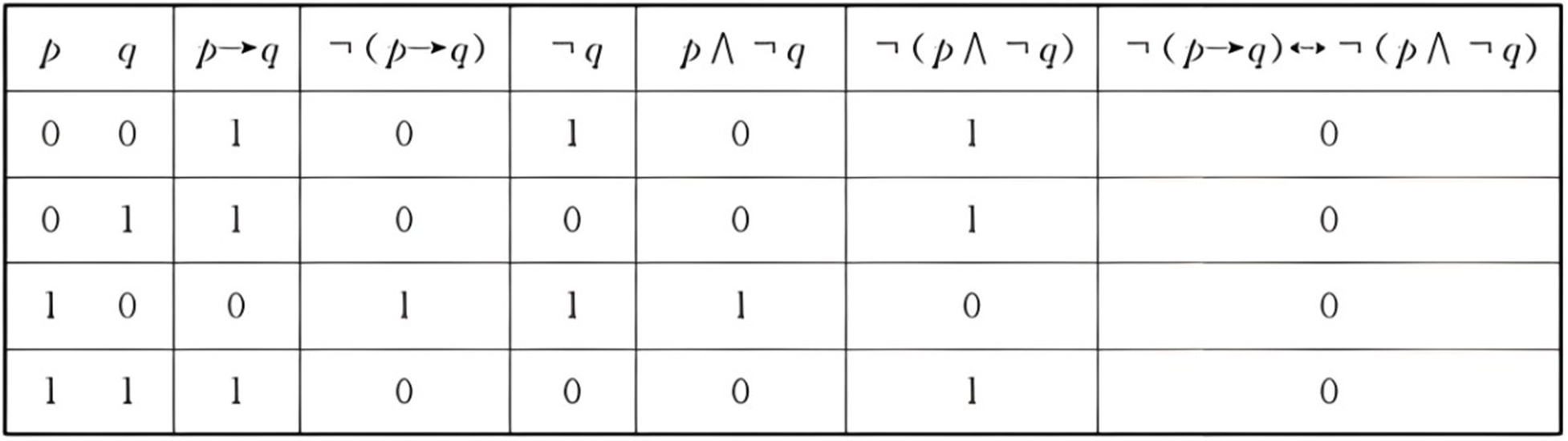
谓词逻辑 – 谓词公式

谓词公式是一种形式语言表达式，也称为合式公式，它按照一定的规则构成。

image-20240716234002100

谓词逻辑 – 量词

定义：在谓词逻辑中，将原子命题进一步细化，分解出“个体、谓词和量词”，来表达“个体与总体的内在联系和数量关系”，这就是谓词逻辑研究内容。
全称量词(universal quantifier) 符号∀表示 表示一切的、凡是的、所 有的、每一 个等。 ∀𝑥 表示定义域中的所有个体 ∀𝑥𝑃(𝑥)表示定义域中的所有个体具有性质𝑃
存在量词(existential quantifier) 符号∃表示， 表示存在、有一个、某些等。 ∃𝑥表示定义域中存在一个或若干个个体， ∃𝑥𝑃(𝑥)表示定义域中存在一个个体或若干个体具有性质 𝑃

全称量词与存在量词的组合

∀𝑥¬𝑃(𝑥) ≡ ¬∃𝑥𝑃(𝑥)

¬∀𝑥𝑃(𝑥) ≡ ∃𝑥¬𝑃(𝑥)

∀𝑥𝑃 𝑥 ≡ ¬∃𝑥¬𝑃 𝑥

∃𝑥𝑃(𝑥) ≡ ¬∀𝑥¬𝑃(𝑥)

谓词逻辑 – 量词的推理规则

中文 英文 表达式
全称量词消去 (Universal Instantiation, UI): (∀𝑥)𝐴(𝑥)→𝐴(𝑦)
全称量词引入 (Universal Generalization, UG): 𝐴 𝑦 → (∀𝑥)𝐴 𝑥
存在量词消去 (Existential Instantiation, EI) (∃𝑥)𝐴(𝑥) → 𝐴(𝑐)
存在量词引入 (Existential Generalization, EG) 𝐴(c) → (∃𝑥)𝐴(𝑥)

谓词逻辑 - 知识表示的方法、特点

  • 谓词公式表示知识的步骤

    • 定义谓词及个体。
    • 变元赋值。
    • 用连接词连接各个谓词，形成谓词公式。

例：用谓词逻辑表示“每个储存钱的人都得到利息”

定义谓词：

save(x)表示x储存钱, interest(x)表示x获得利息

则该知识可以表示为：

(∀x) ( save(x) ) → interest(x) )

优点 ①自然性②精确性③严密性④容易实现
局限性 ①不能表示不确定的知识②组合爆炸③效率低
应用 ①求解化学方面问题的QA3系统②STRIPS机器人行动规划系统③FOL机器证明系统

产生式表示法 – 定义

产生式表示法：又称为产生式规则（production rule）表示法。通常用于表示事实、规则以及它们的不确定性度量，适合于表示“事实性知识”和“规则性知识”。美国数学家波斯特在1943首先提出“产生式”这一术语

1972年，纽厄尔和西蒙在研究人类的认知模型中开发了基于规则的产生式系统。认知心理学(以西蒙、纽厄尔为代表)人的一切行为过程是由内部信息处理的过程所驱动。人类对于外部世界的感知、思考、决策和行为都是通过信息处理的方式来完成的。具体来说，信息处理过程可以分为“感知、注意、认知、记忆、思考、决策”几个阶段。

image-20240716234140627

产生式知识表示法 – 分类

规则知识 确定性规则知识的产生式表示 •基本形式： IF P THEN Q 或者： P → Q例：r4：IF动物会飞AND会下蛋THEN该动物是鸟
不确定性规则知识的产生式表示 •基本形式： IF P THEN Q （置信度） 或者： P → Q（置信度）例：IF发烧THEN感冒（0.6）
事实性知识 确定性事实性知识的产生式表示 •三元组表示：（对象，属性，值） 或者：（关系，对象1，对象2） 例：老李年龄是40岁：（Li，age，40）老李和老王是朋友：（friend，Li，Wang）
不确定性事实性知识的产生式表示 •四元组表示：（对象，属性，值，置信度） 或者： （关系，对象1，对象2，置信度） 例：老李年龄很可能是40岁：（Li，age，40，0.8）老李和老王不大可能是朋友：（friend，Li，Wang，0.1）
  • 产生式不仅可以表示精确的知识，还可以表示不精确知识。
  • 产生式匹配可以是精确的，也可以是不精确的，只要按某种算法求出的相似度落在预先指定的范围内就认为是可匹配的。

产生式知识系统的案例 - 动物识别系统

例如：动物识别系统——识别虎、金钱豹、斑马、长颈鹿、鸵鸟、企鹅、信天翁等七种动物的产生式系统。

image-20240716234224051

框架表示法 – 框架理论、框架定义

1975年，美国明斯基提出了框架理论：人们对现实世界中各种事物的认识都是以一种类似于框架的结构存储在记忆当中。

框架表示法：一种结构化的知识表示方法，已在多种系统中得到应用。框架（frame）：一种描述所论对象（一个事物、事件或概念）属性的数据结构。一个框架由若干个被称为“槽”（slot）的结构组成，每一个槽又可根据实际情况划分为若干个“侧面”（faced）。一个槽用于描述所论对象某一方面的属性。一个侧面用于描述相应属性的一个方面。槽和侧面所具有的属性值分别被称为槽值和侧面值。

框架表示法 – 框架的表示形式与结构

框架的一般表示形式：

image-20240716234412248

用框架表示知识的例子

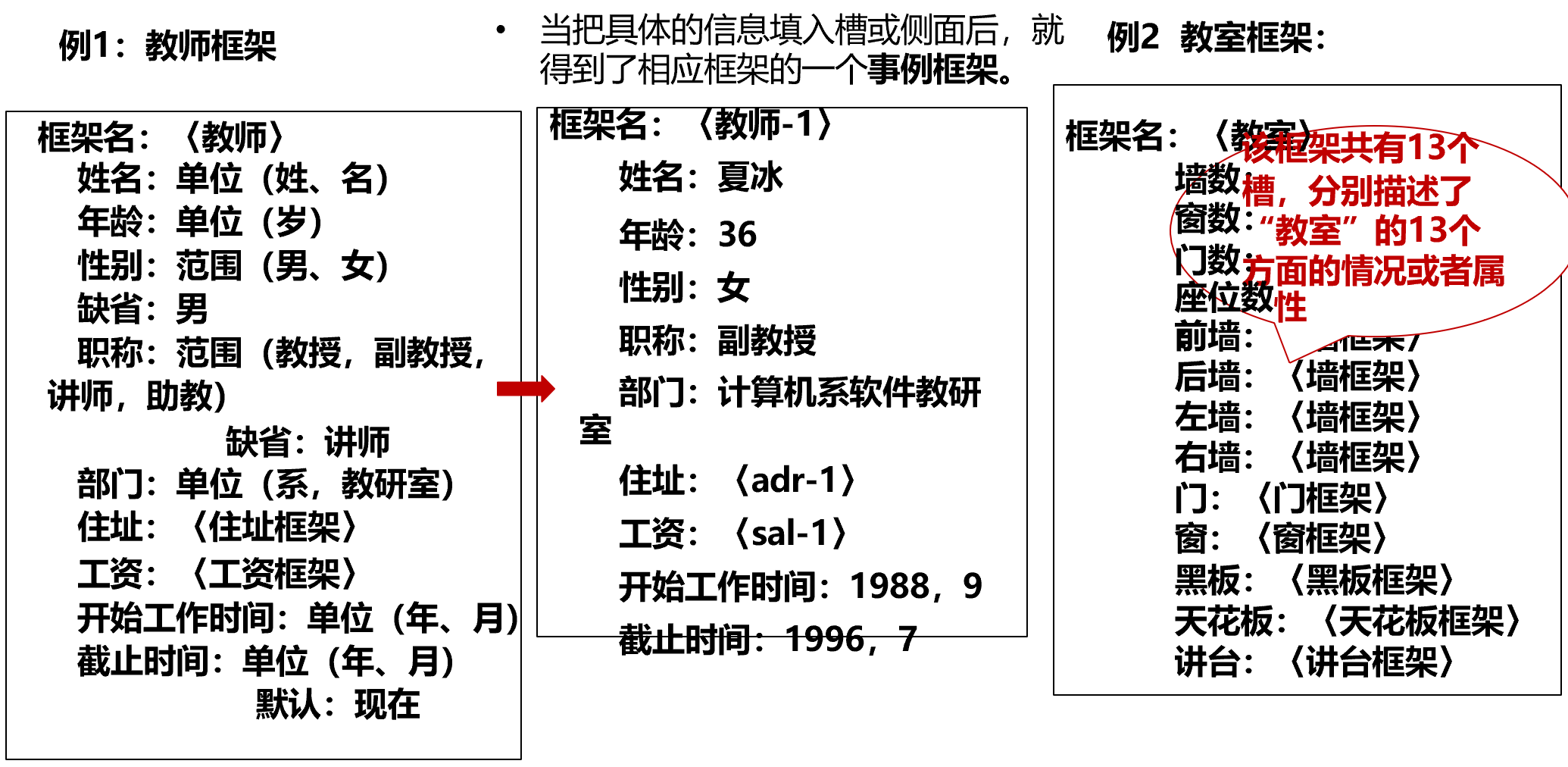
image-20240716234429579

框架表示法的特点

  • 框架表示法的特点

    • 结构性：便于表达结构性知识，能够将知识的内部结构关系及知识间的联系表示出来。
    • 继承性：框架网络中，下层框架可以继承上层框架的槽值，也可以进行补充和修改。
    • 自然性：框架表示法与人在观察事物时的思维活动是一致的。