Dijkstra搜索算法原理及其程序实现
前言
本文算是我学习这个算法的学习记录,因此我会更加侧重于程序实现的讲解,因为原理相关的内容我已经非常熟悉了,并且Dijkstra算法需要有一定图论相关的知识,不过没必要完全系统地学会,只需要知道无向图,有向图,邻接矩阵相关的概念就行了。
下面我将会以在图中寻找一个节点(称为“源节点”)到所有其它节点的最短路径的例子进行讲解,在文章的末尾将给出程序完整的Python与C++实现
基础知识
下面的相关知识,是你在编程前必须要知道的
Dijkstra 算法从指定的节点(源节点)出发,寻找它与图中所有其它节点之间的最短路径。
Dijkstra 算法会记录当前已知的最短路径,并在寻找到更短的路径时更新。
一旦找到源节点与其他节点之间的最短路径,那个节点会被标记为“已访问”并添加到路径中。
重复寻找过程,直到图中所有节点都已经添加到路径中。这样,就可以得到从源节点出发访问所有其他节点的最短路径方案。
Dijkstra 只能用在权重为正的图中,因为计算过程中需要将边的权重相加来寻找最短路径。
Dijkstra算法可以看成是贪心策略与广度优先算法的结合,在每一次节点扩散的时候,都需要进行权重(可以理解为距离)大小的比较,因此存在负权重,则可能在之后的计算中得到总权重更小的路径,从而影响之前的结果,用一个比较实际的例子就是绕的路更多,反而路线更短了,这显然是不符合实际的
算法实现
假设有下面这个图,我们设置源节点 src=0,为了求解src到其他节点(1~8)的最短距离,按照下面的步骤
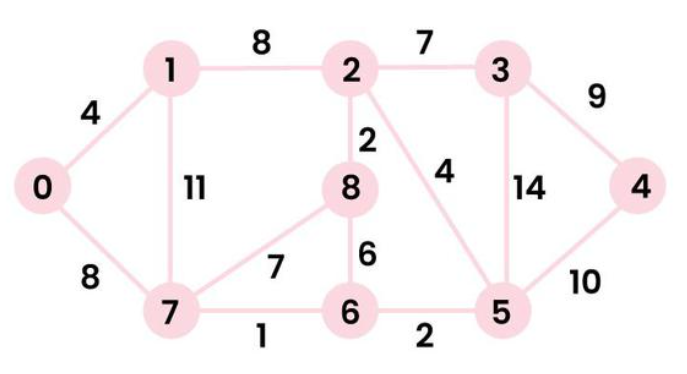 d
d
- 这里我们需要维护两个数组isset和dist,其中isset数组用来表示对应节点是否已经拓展,初始化为
false。dist数组初始化为{0, INF, INF, INF, INF, INF, INF, INF},这个数组的下标用来表示节点,下标对应的内容表示src节点到其他节点的最短距离,这里选取的src=0,由于节点到自身的距离始终为0,所以这里dist[0]=0,其他初始化为INF(无穷大)
1 | #参数初始化 |
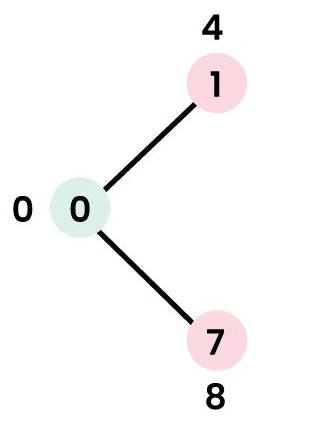
- 现在我们需要从dist数组中找到距离值最小且isset数组值为false的节点,由于是第一次扩展节点,所以距离值最小的一定是src节点。扩展后将src节点下标对应的isset数组的内容改为
true,0 的相邻顶点是 1 和 7,更改距离值.
1 | #寻找dist最小值 |
| isset | true | false | false | false | false | false | false | false | false |
|---|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dist | 0 | 4 | INF | INF | INF | INF | INF | 8 | INF |
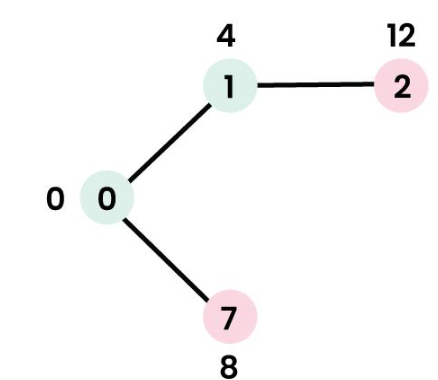
- 接着从dist数组中找出最小值且isset数组值为false的节点进行扩展,在第二步得到的结果中,dist最小值对应的是节点
1,因此对节点1的相邻节点进行扩展,然后将节点2的值更改为12,为什么是12而不是8?,参照上面完整的图,节点0到节点1的距离是4,节点1到节点2的的距离是8,所以这里的12指的是经过0-1-2的累加距离4+8=12,后面每次扩展的时候,都要进行距离的累加
1 | # 整个算法最核心的部分就是这个if的判断语句 |
经过上述的变化后,数组的值变更为以下的结果
| isset | true | true | false | false | false | false | false | false | false |
|---|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dist | 0 | 4 | 12 | INF | INF | INF | INF | 8 | INF |
- 重复以上的步骤,这里需要注意如果新扩展到的dist数组的值比旧的dist数组的值要大,那么就不更新dist数组
- 最终可以得到一个src节点到其他节点的最小生成树

完整程序实现
接下来将代码整合成一个完整版
Python版本
1 | import numpy as np |
C++版本
1 |
|
参考资料
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 木人舟的博客!
评论
ValineDisqus
